Crystals are natural or synthetic solids that have their atoms arranged in an organized, repeating pattern. These patterns create a framework for understanding how crystals form and how they look.
Crystal systems are the broad categories that group crystals based on their overall shape and symmetry. There are seven crystal systems, and each system has its unique features. The systems are based on the lengths and angles of the axes that define the shape of a crystal. These axes are like imaginary lines you can draw to describe the crystal's structure.
| Crystal System | Crystal Class | Point Group | Symmetry Characteristics |
|---|---|---|---|
| Triclinic | Pedial | 1 | No symmetry; only identity. |
| Pinacoidal | 1 | Inversion center only. | |
| Monoclinic | Sphenoidal | 2 | One 2-fold rotation axis. |
| Domatic | m | One mirror plane. | |
| Prismatic | 2/m | One 2-fold axis and one mirror plane. | |
| Orthorhombic | Rhombic-Disphenoidal | 222 | Three 2-fold rotation axes. |
| Rhombic-pyramidal | mm2 | Two mirror planes and one 2-fold axis. | |
| Rhombic-dipyramidal | mmm | Three mutually perpendicular mirror planes. | |
| Tetragonal | Tetragonal-pyramidal | 4 | One 4-fold rotation axis. |
| Tetragonal-disphenoidal | 4 | One 4-fold inversion axis. | |
| Tetragonal-dipyramidal | 4/m | One 4-fold axis and one mirror plane. | |
| Tetragonal-trapezohedral | 422 | One 4-fold axis and two 2-fold axes. | |
| Ditetragonal-pyramidal | 4mm | One 4-fold axis and four mirror planes. | |
| Tetragonal-scalenohedral | 42m | One 4-fold inversion axis and two mirror planes. | |
| Ditetragonal-dipyramidal | 4/mmm | One 4-fold axis, four 2-fold axes, and five mirror planes. | |
| Hexagonal-Trigonal | Trigonal-pyramidal | 3 | One 3-fold rotation axis. |
| Rhombohedral | 3 | One 3-fold inversion axis. | |
| Trigonal-trapezohedral | 32 | One 3-fold axis and three 2-fold axes. | |
| Ditrigonal-pyramidal | 3m | One 3-fold axis and three mirror planes. | |
| Ditrigonal-scalenohedral | 3m | One 3-fold inversion axis and three mirror planes. | |
| Hexagonal-Hexagonal | Hexagonal-pyramidal | 6 | One 6-fold rotation axis. |
| Trigonal-dipyramidal | 6 | One 6-fold inversion axis. | |
| Hexagonal-dipyramidal | 6/m | One 6-fold axis and one mirror plane. | |
| Hexagonal-trapezohedral | 622 | One 6-fold axis and six 2-fold axes. | |
| Dihexagonal-pyramidal | 6mm | One 6-fold axis and six mirror planes. | |
| Ditrigonal-dipyramidal | 6m2 | One 6-fold inversion axis and six mirror planes. | |
| Dihexagonal-dipyramidal | 6/mmm | One 6-fold axis, six 2-fold axes, and seven mirror planes. | |
| Cubic | Tetartoidal | 23 | Three 2-fold axes and 3-fold axes. |
| Diploidal | m3 | Inversion center and 3-fold axes. | |
| Gyroidal | 432 | Four 3-fold axes and three 2-fold axes. | |
| Hexoctahedral | 43m | Four 3-fold axes and six mirror planes. | |
| Hexoctahedral | m3m | Four 3-fold axes, three 2-fold axes, and nine mirror planes. | |
| Icosahedral | Ih | 532 | Five 2-fold, three 3-fold, and two 5-fold axes. |
Crystal classes are more specific categories that describe the detailed symmetry of crystals. While crystal systems focus on the general shape, crystal classes go deeper into how the crystal's faces and angles are arranged.
There are 32 crystal classes, and they are grouped under the seven crystal systems. These classes explain how the symmetry elements, such as rotation axes and mirror planes, combine in different ways to create unique patterns.
Understanding crystal systems and classes helps scientists identify minerals, design new materials, and even study properties like light reflection or strength. It is like having a map to understand the building blocks of solid materials.
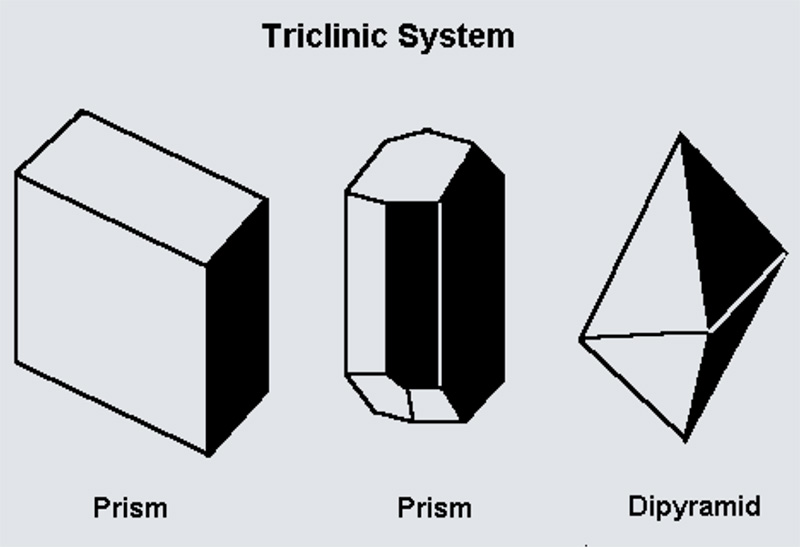

The Pedial class has no symmetry at all. It’s the simplest crystal class, where the unit cell has no planes of reflection, no axes of rotation, and no inversion centers. Think of it as completely asymmetric, like a box twisted in every direction.

The Pinacoidal class is slightly more symmetric than Pedial. It has a single symmetry element: an inversion center. This means every point in the crystal has an equivalent point directly opposite through the center of the crystal. It’s still triclinic, but with this one added symmetry.
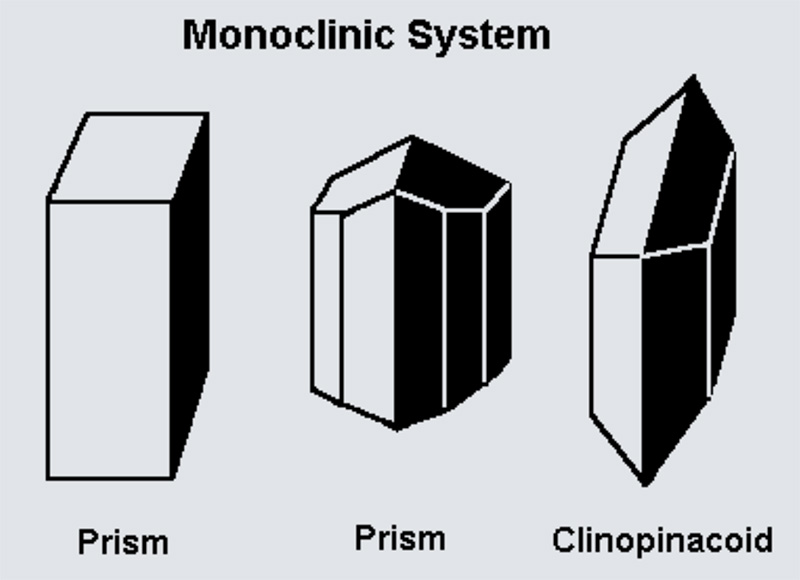
A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal lengths, as in the orthorhombic system. They form a parallelogram prism. Hence two pairs of vectors are perpendicular (meet at right angles), while the third pair makes an angle other than 90°.

The Sphenoidal class has a single 2-fold rotational symmetry. This means the crystal can be rotated by 180° around one axis, and it looks the same. It's one of the simpler monoclinic classes with minimal symmetry.

The Domatic class is characterized by the presence of a single mirror plane. This means one side of the crystal is a mirror image of the other across this plane. It gives the crystal partial symmetry while retaining a monoclinic structure.

The Prismatic class combines a 2-fold rotation axis and a perpendicular mirror plane. This means the crystal can be rotated by 180° around one axis and will still look the same, and one side reflects onto the other across the mirror plane.
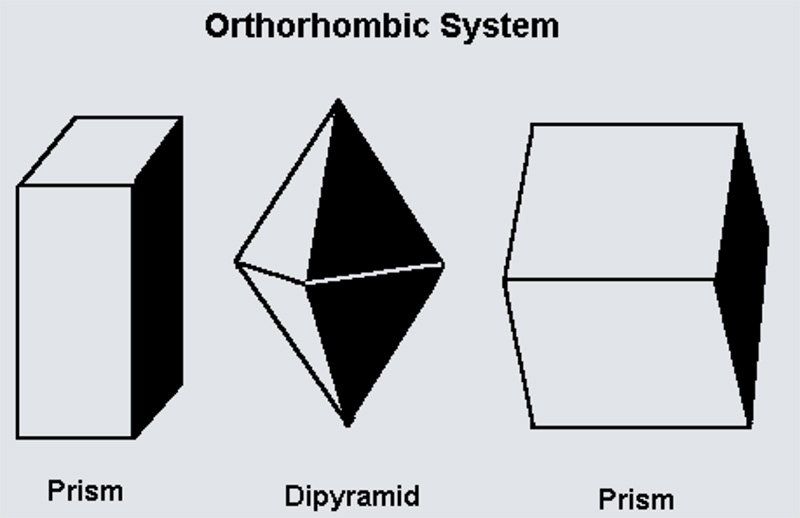
Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base (a by b) and height (c), such that a, b, and c are distinct. All three bases intersect at 90° angles, so the three lattice vectors remain mutually orthogonal.

The Sphenoidal class has three 2-fold rotational axes, each aligned with the crystal’s principal directions (X, Y, and Z). It has no mirror planes or inversion centers, resulting in limited symmetry.

The Pyramidal class is characterized by two perpendicular mirror planes and a single 2-fold rotation axis. This gives it moderate symmetry, where certain faces and directions are mirrored or repeated.

The Dipyramidal class has the highest symmetry in the orthorhombic system. It features three mutually perpendicular mirror planes and three 2-fold rotational axes. This makes it highly symmetric and balanced in all directions.
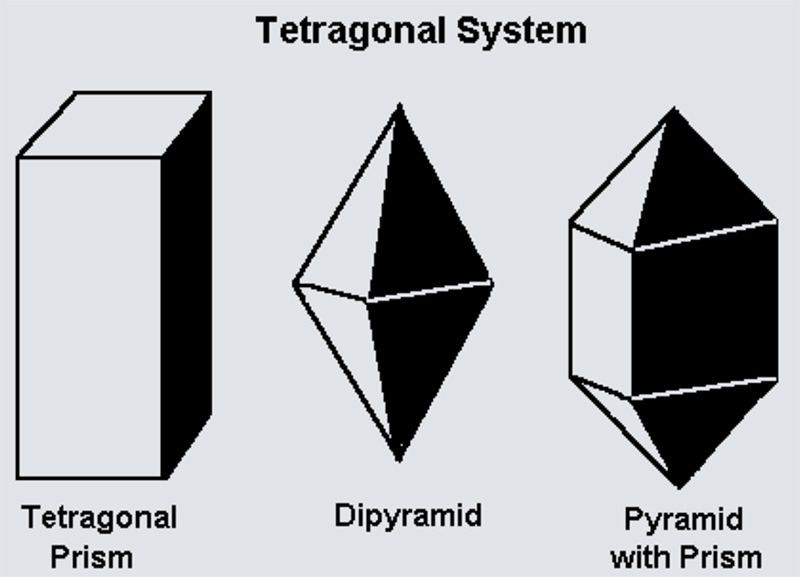
Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base (a by a) and height (c, which is different from a).

The Tetragonal Pyramidal class features a single 4-fold rotational axis, meaning the crystal can be rotated by 90° and look the same.

The Tetragonal Disphenoidal class has a single 4-fold rotoinversion axis, where the crystal appears the same after a 90° rotation followed by inversion.

The Tetragonal Dipyramidal class combines a single 4-fold rotational axis with a perpendicular mirror plane, adding higher symmetry to the tetragonal structure.

The Tetragonal Trapezohedral class features a 4-fold rotational axis and two perpendicular 2-fold axes, giving it intermediate symmetry in the tetragonal system.

The Ditetragonal Pyramidal class combines a 4-fold axis with four mirror planes extending radially, providing high symmetry.

The Tetragonal Scalenohedral class combines a 4-fold rotoinversion axis with mirror planes to provide high symmetry.

The Ditetragonal Dipyramidal class has a 4-fold rotational axis combined with multiple perpendicular mirror planes, resulting in the highest symmetry in the tetragonal system.
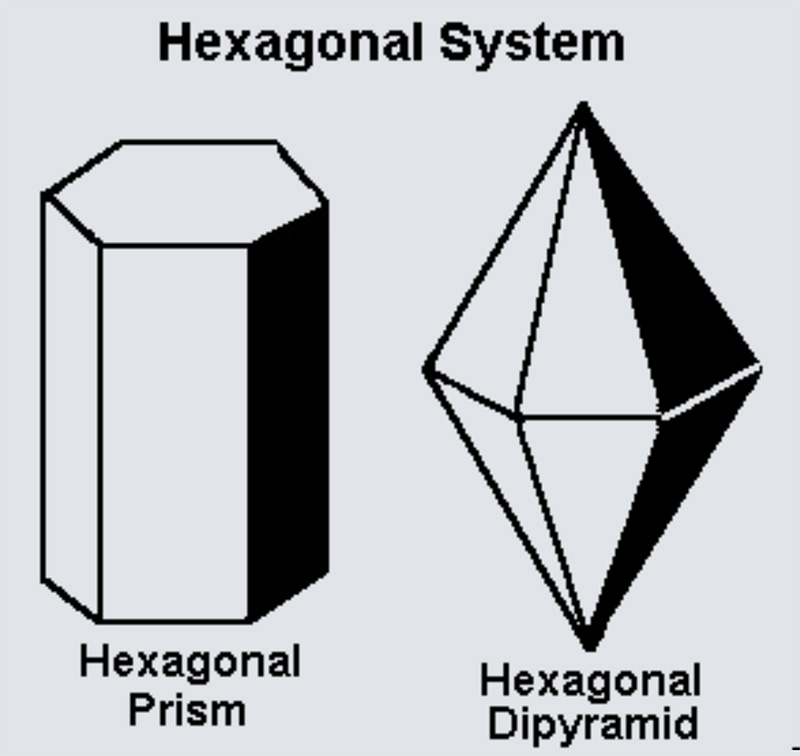
The hexagonal crystal family is one of the six crystal families, which includes two crystal systems (hexagonal and trigonal) and two lattice systems (hexagonal and rhombohedral). While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent.

A trigonal-pyramidal structure describes a molecule with a central atom bonded to three atoms in a triangular base and one lone pair at the top, forming a pyramid shape. An example is ammonia (NH₃), with bond angles around 107°.

Also known as the trigonal system, it consists of a unit cell where all three axes are of equal length (a = b = c) and intersect at equal angles that are not 90°, forming a rhombohedron. This is represented as hR (hexagonal rhombohedral) in Pearson notation.

The trigonal-trapezohedral class is part of the trigonal crystal system, featuring a threefold rotational symmetry with perpendicular twofold axes. Its shape resembles a trigonal trapezohedron, a polyhedron with six congruent rhombic faces. This symmetry is found in minerals like alpha-quartz and cinnabar.

The ditrigonal-pyramidal class is a category within the trigonal crystal system, characterized by a threefold rotational axis and three vertical mirror planes. This symmetry leads to crystal forms such as the ditrigonal pyramid, which has six triangular faces meeting at a point. Minerals like tourmaline and alunite commonly exhibit this symmetry.

The ditrigonal-scalenohedral class is part of the trigonal crystal system, characterized by a threefold rotational axis, three perpendicular twofold axes, and a center of symmetry. This symmetry results in complex crystal forms like the scalenohedron, featuring twelve identical scalene triangular faces. Minerals such as calcite and corundum commonly exhibit this symmetry.

The hexagonal-pyramidal class belongs to the hexagonal crystal system and is characterized by a single sixfold rotational axis without additional symmetry elements. This results in crystal forms such as hexagonal pyramids, which have six triangular faces converging at a point. Minerals like nepheline and cancrinite often exhibit this symmetry.

The trigonal-dipyramidal class is part of the hexagonal crystal system, characterized by a sixfold rotoinversion axis (appearing as a threefold axis) and a mirror plane perpendicular to this axis. This symmetry leads to crystal forms such as the trigonal dipyramid, featuring six triangular faces arranged symmetrically around a central axis. Minerals like cesanite and laurelite exhibit this symmetry.

The hexagonal-dipyramidal class is part of the hexagonal crystal system, characterized by a sixfold rotational axis (6-fold) perpendicular to a mirror plane, with a center of symmetry. This symmetry leads to crystal forms such as hexagonal dipyramids, featuring twelve identical triangular faces arranged symmetrically around the central axis. Minerals like apatite and vanadinite commonly exhibit this symmetry.
The hexagonal-trapezohedral class is part of the hexagonal crystal system, characterized by a sixfold rotational axis and six twofold axes perpendicular to it. This symmetry leads to crystal forms like the hexagonal trapezohedron, featuring twelve congruent kite-shaped faces. Minerals such as high-temperature quartz (beta-quartz) and kalsilite exhibit this symmetry.

The dihexagonal-pyramidal class is part of the hexagonal crystal system, characterized by a sixfold rotational axis and six vertical mirror planes. This symmetry results in crystal forms like the dihexagonal pyramid, featuring twelve triangular faces converging at a point. Minerals such as wurtzite and greenockite commonly exhibit this symmetry.

In this class, the principal axis is a sixfold axis of rotatory inversion, which can be easily confused with a threefold axis perpendicular to a mirror plane. However, these symmetries are distinct and are often listed separately in crystallographic classifications.

The dihexagonal-dipyramidal class is the highest symmetry class in the hexagonal crystal system, characterized by a sixfold rotational axis, six perpendicular twofold axes, seven mirror planes, and a center of symmetry. This symmetry leads to crystal forms such as the dihexagonal dipyramid, featuring twenty-four identical triangular faces arranged symmetrically around the central axis. Minerals like beryl, molybdenite, and graphite commonly exhibit this symmetry.


The tetartoidal class is one of the five crystal classes within the cubic (isometric) crystal system. It is characterized by tetrahedral symmetry, specifically the point group 23 in Hermann–Mauguin notation. Minerals such as gersdorffite crystallize in this symmetry class.

The diploidal class is one of the five crystal classes within the cubic (isometric) crystal system. It is characterized by a combination of threefold and twofold rotational axes, along with mirror planes, leading to a centrosymmetric structure. Minerals such as pyrite crystallize in this symmetry class.

The gyroidal class is one of the five crystal classes within the cubic (isometric) crystal system. It is characterized by a combination of four threefold rotational axes and three fourfold rotoinversion axes, leading to enantiomorphic (chiral) structures. Minerals such as petzite crystallize in this symmetry class.

The hextetrahedral class is part of the cubic (isometric) crystal system, characterized by four threefold rotational axes, three fourfold rotoinversion axes (appearing as twofold axes), and six mirror planes. This symmetry leads to crystal forms such as the tetrahedron, tristetrahedron, and deltoidal dodecahedron. Minerals like sphalerite and sodalite commonly exhibit this symmetry.

The hexoctahedral class is the highest symmetry class within the cubic (isometric) crystal system, characterized by three fourfold rotational axes, four threefold axes, and six twofold axes, along with multiple mirror planes and a center of symmetry. This extensive symmetry leads to complex crystal forms such as the hexoctahedron, which has 48 triangular faces, and the tetrahexahedron, featuring 24 faces. Minerals like fluorite and galena commonly exhibit this symmetry.
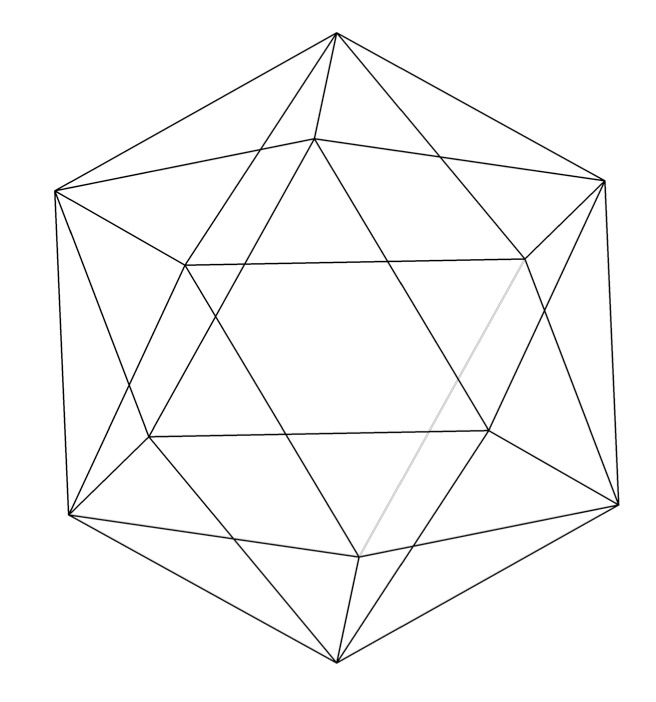

Icosahedrite is the first known naturally occurring quasicrystal, with the composition Al₆₃Cu₂₄Fe₁₃. Discovered in 2009 in the Khatyrka meteorite from Russia's Koryak Mountains, it exhibits an ordered atomic structure without periodic repetition, specifically icosahedral symmetry. This finding challenged the prior belief that quasicrystals could only be synthesized in laboratories.